SISTEMA DE ECUACIONES

 

Es la reunión de dos o más ecuaciones que deben satisfacerse para los mismos valores de las incógnitas.

SOLUCIÓN DEL SISTEMA

Es el conjunto de valores numéricos o literales que satisfacen las ecuaciones.

Los sistemas de ecuaciones pueden ser Numéricos o Literales, según la naturaleza de las ecuaciones que los constituyen.

 

 

 

 

 

 

 

 

 

 Cuando la solución de un sistema es única, es decir, existe un sólo valor para cada incógnita, el sistema se llama Determinado. Por lo general el número de incógnitas es igual al número de ecuaciones.

 

 

RESOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES CON DOS INCÓGNITAS

 

Para la resolución de sistemas de ecuaciones de primer gradocon dos incógnitas se aplican métodos de eliminación, queconsisten esencialmente en eliminar una de las incógnitas yobtener una sola ecuación de una incógnita.

 

Los métodos de eliminación más usuales son:

•Método por Sustitución

•Método por Igualación

•Método por Reducción  

•Método Gráfico 

•Método por Determinantes 

 

 

MÉTODO POR SUSTITUCIÓN REGLA

Para la eliminación por Sustitución, se siguen los siguientes pasos:

 

1. Se despeja una de las incógnitas de una de las ecuaciones del sistema.

2. Se sustituye este valor obtenido en la otra ecuación.

3. Se resuelve la ecuación de primer grado con una incógnita que así se obtiene.

4. El valor obtenido se sustituye en cualquiera de las ecuaciones originales.

5. Se comprueba la solución, sustituyendo los valores obtenidos en las ecuaciones dadas. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  MÉTODO POR IGUALACIÓNREGLA

Para la eliminación por Igualación, se siguen los siguientes pasos:

 

1. Se despeja una de las incógnitas en cada una de las ecuaciones, ésta debe ser la misma en ambas.

2. Se igualan los dos valores de las incógnitas así obtenidas.

3. Se resuelve la ecuación de primer grado con una incógnita que así se obtiene.

4. El valor obtenido se sustituye en cualquiera de las ecuaciones originales.

5. Se comprueba la solución, sustituyendo los valores obtenidos en las ecuaciones dadas.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 MÉTODO POR REDUCCIÓNREGLA:

 

Para la eliminación por Reducción, se siguen los siguientes pasos:

 

1. Determinamos que variable eliminar, luego el coeficiente de dicha variable en la ecuación (1) se ha de multiplicar por la ecuación (2), y el coeficiente de la variable a eliminar de la ecuación (2) se multiplica por la ecuación (1). Procurando que los coeficientes de la variable a eliminar tengan signos contrarios.

2. Reducimos los términos y resolvemos la ecuación resultante.

3. El valor obtenido se sustituye en una de las ecuaciones originales.

4. Se comprueba la solución, sustituyendo los valores obtenidos en las ecuaciones dadas

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

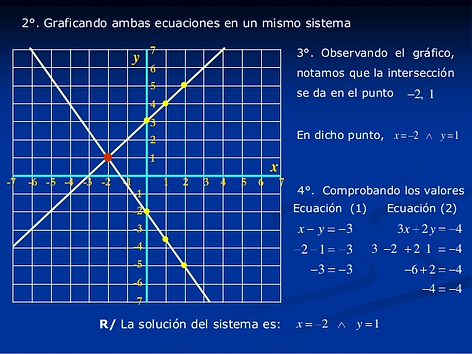
MÉTODO GRÁFICO

 

Resolver gráficamente un sistema de dos ecuaciones lineales con dosincógnitas, consiste en hallar el punto de intersección de las gráficasde Las ecuaciones lineales, para ello es necesario graficar las dosecuaciones en un mismo sistema de coordenadas cartesianas.

 

1. Se despeja la variable “y” en cada una de las ecuaciones, y luego se elabora una tabla, asignándole valores      a “x”.

2. Se grafican ambas ecuaciones en un mismo plano cartesiano.

3. Se observa el punto de intersección de ambas gráficas.

4. Se comprueba la solución, sustituyendo los valores del punto de intersección observado en las ecuaciones      dadas.