TRINOMIO CUADRADO PERFECTO

EJEMPLO 1: (Términos positivos)


x2  +  6x  +  9 = (x + 3)2

x                3
      2.3.x
         6x

Busco dos términos que sean "cuadrado" de algo. Son: x2 y 9. Entonces "bajo" la x y el 3 (las bases). Luego verifico 2.x.3 = 6x ("doble producto del primero por el segundo"). Dió igual que el otro término. El polinomio es un cuadrado "perfecto". El resultado de la factorización es la suma de las bases elevada al cuadrado: (x + 3)

 

                      TRINOMIO POR SUMA Y RESTA

 

 

 

 

 

 

 

 

 

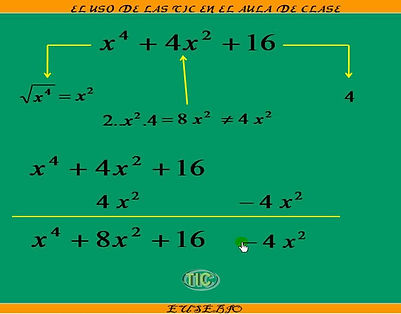
Ejemplo:  Factorar    x^4 +x^2y^2 +y^4

 

1º) Comprobar si el trinomio es cuadrado perfecto:

raíz cuadrada de x^4 = x^2      ;     Raíz cuadrada de y^4 = y^2

el 2º  término debiera ser  2(x^2)(y^2) = 2x^2 y^2

Comparando 2º término (2x^2y^2) – (x^2y^2) = x^2y^2  lo que le falta

 

2º) Convirtiendo a trinomio cuadrado  perfecto, sumando la diferencia que falta al 2º término y restando la misma diferencia al trinomio dado, así:

x^4   +  x^2y^2  + y^4                     (Trinomio original)

.       +  x^2y^2              – x^2y^2     (sumando y restando lo que le hace falta)

x^4 +2x^2y^2 +y^4  -x^2y^2  = (x^4 +2x^2y^2 +y^4) -x^2y^2 (resultado de convertir el trinomio)

 

3º) Factorando el trinomio cuadrado perfecto Caso III:

(x^4 +2x^2y^2 +y^4)  – x^2y^2 =  (x^2 + y^2)^2 – x^2y^2

 

4º) Factorando la diferencia de cuadrados Caso IV:

(x^2 + y^2)^2 – x^2y^2  = (x^2 +y^2 +xy)(x^2y^2 -xy)

Ordenado sería = (x^2 +xy +y^2)(x^2 -xy+y^2) <– Solución

 

 

               Trinomio de la forma x2 + bx + c

 

 

 

 

 

 

 

   Veamos algunos ejemplos sobre este caso.

 

1)     X2 + 7x + 10.

 

Primero construimos los dos binomios, los cuales se encuentran buscando la raíz cuadrada del primer término.

 

 (x  )  (x  )

 

El primer signo del binomio será el signo que tiene el segundo término que en este caso es positivo, y el segundo será el que nos queda de operar los signos del segundo término y del tercer término, en este caso también es positivo, por lo tanto nos quedara.

 

(x +   )  (x +   )

 

Como los signos que tienen los binomios en los medios son iguales buscaremos dos números que multiplicados sean igual al tercer término del trinomio que es 10; y cuya suma sea igual al valor absoluto del segundo término que es 7.

 

 

Entonces los números serian: (5 y 2)

 

La regla nos dice que el número más grande será el segundo término del primer binomio y el menor será el segundo término del segundo binomio, por lo tanto nos queda.

 

 (x + 5  )  (x +  2 ) respuesta.

 

 

                 trinomio de la forma ax^2 +bx +c:

 

 

 

 

 

 

 

–Antes de descomponer el trinomio en dos factores binomios,

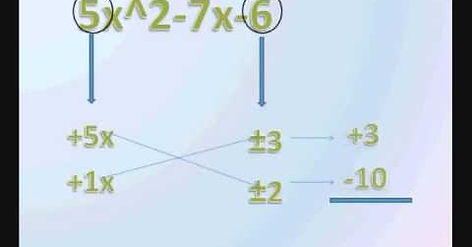
se procede así: como ejemplo: 6x^2 -7x -3

1°) Se multiplica el coeficiente del primer término ” 6 ” por todo el trinomio, dejando el producto del 2° término indicado:

6(6x^2 -7x +3) = 36x^2 -6(7x) -18

2°)   Se ordena tomando en cuenta que 36x^2 = (6x)^2    y  6(-7x) = -7(6x), escribiéndolo de la siguiente manera:  (6x)^2 -7(6x) -18

3°) Luego se procede a factorar  (6x)^2 -7(6x) -18 como un problema del Caso VI. con una variante que se explica en el Inciso 6°

4°) Se forman 2 factores binomios con la raíz cuadrada del primer término del trinomio:   (6x-   )(6x+  )

5°) Se buscan dos #s cuya diferencia sea -7   y cuyo producto sea -18 ;  y esos #s  son -9  y  +2   porque:  -9 +2 = -7   y   (-9)(2) = -18 –>  =  (6x-9)(6x+2)

6°) Aquí está la variante:  Como al principio multiplicamos el trinomio por “6”, entonces ahora los factores binomios encontrados, los dividimos entre  “6”

(6x-9)(6x+2) / 6   ;  como ninguno de los binomios es divisible entre “6” entonces descomponemos el “6” en dos factores (3  y 2), de manera que uno divida a un factor binomio y el segundo divida al otro. Así:  (6x-9) / 3    y  (6x+2) / 2 , y estos cocientes quedarían así:  (2x-3)(3x+1). que sería la Solución.